Models of Inelastic Accretion
The purpose is to investigate analytical models of accretion, particularly inelastic, which may be the same thing as dynamic plastic deformation in the grand scheme. One is slanted from the physics perspective, the other from engineering mechanics. Ultimately, while the latter description is correct from a continuum material standpoint, the former seems to embrace the notion of free body participation which would exist internally in some fashion in any real collapse.
The models under discussion are 1D unless otherwise indicated. The development here will focus primarily on an analytic treatment in the continuous domain, but the relation to discrete models and their inner workings will be discussed, too. There is much crossover and tie-in, and it's natural to expect one to validate the others here and there. Finally, this can also be useful in working towards models of granular collapse, which is the specific focus of yet another thread.
What follows is the original post in the toy simulacra thread. It's very basic and really gives no indication of the depth I now wish to explore, time permitting.
Uniform density ρ given total height H and mass M:
ρ = M/H
The change of mass accumulated with respect to time:
dm/dt = ρdy/dt = ρv
Conservation of momentum in incremental inelastic collision:
mv = (m + Δm)(v + Δv)
Multiplying out quantities in parentheses:
mv = mv + mΔv + vΔm + ΔmΔv
Eliminating original momentum from both sides:
0 = mΔv + vΔm + ΔmΔv
Dropping second order quantity:
mΔv = -vΔm
Dividing both sides by Δt, the increment of time:
mΔv/Δt = -vΔm/Δt
Allow increment to go to infinitesimal:
mdv/dt = -vdm/dt
Substitute expressions for instantaneous acceleration and mass accumulation rate:
ma = -ρv2
Thus the resistive force due to inelastic accretion is:
Fr = -ρv2
where the negative sign indicates the force opposes the direction of motion.
If the moving portion of the mass is subject to gravitational force, then the total force on the moving portion at a given time is
F = mg - ρv2
where m, ρ, and v are all functions of time.
Acceleration is therefore:
a = g - (ρ/m)v2
Since the instantaneous upper block mass m is:
m = ∫ρdy evaluated on [0,y] = ρy
the above relation a = g - (ρ/m)v2 becomes:
a = g - v2/y
This is Cherepanov's equation of motion. Wow, that was easy! Now, how does one get asymptotic approach of acceleration to g/3 from this?
g/3 or g/2 asymptote, who's right?
The treatment above probably parallels the work of shagster (formerly at physorg) pretty closely. Shagster, in turn, used Cherepanov as a springboard. For those who don't know, Cherepanov is both (I believe) a respected scientist and (I know for a fact) pretty far out there in terms of unconventional thought. Bazant was dismissive of Cherepanov's fracture theories, and I have to agree if not for all the same reasons; in many respects the 'observations' he was comparing theory against were further from the mark than Bazant's or others, so a good fit with imaginary observations simply makes a bad fit with reality.
However improbable or even bizarre some of Cherepanov's ideas may be, the equation of motion above - which appears in one of his articles - is quite solid, if a bit limited. I only refer to it as Cherepanov's equation because his is the only published derivation to my knowledge (which is weak). A search for "inelastic accretion" nets mostly the physics of planetary formation, various citations to ONE NASA paper on inelastic accretion in granular flow, and ME.
It seems to be an underdeveloped subject. I knew about and read both the shagster/Cherepanov derivations without paying much attention to the details. In another essay recently, I mentioned the convergence of acceleration to g/3, and it reminded me of the discussions here on the subject which remained somewhat unresolved. I decided to take a look at the problem from scratch and come up with something which showed why this was expected. Bazant said his treatment led to a g/3 limit. Greening at physorg says the Cherapanov formulation does the same. Both the simulations of this thread and the Greening style discrete algebraic method say g/3. Seffen says g/2. Who's right?
The first step in getting an answer is doing the mechanics. I did it my own way above and it comes to the Cherapanov result. But this was a first pass, momentum only. Naturally, this is a good time to review the various papers again to follow the momentum-only derivations and note the differences. The actual work on inelastic accretion seems to be subsumed under other headings but is rare in any case. Conversations about this have tended to be muddled, I'd like to sort it out.
Then, if there are any deficiencies in the current models, correct them. Extend it if possible.
There may be a curious inversion of the relationship between the toy simulacra and the analytical models going forward: the former will be used to validate the latter.
A Momentum-only Model
The first inadequacy is the model being momentum-only. If this is where Cherapanov stopped the conventional dynamic analysis, he stopped too soon. Nevertheless, it's a formidable bridge to cross. The analysis above makes clear the contrivance that accreted matter is subject to gravitational force but unaccreted matter is left undefined in this respect. A profoundly unphysical situation for the most part; it's hard to even imagine a material or system which satisfies the implied constraints.
Stationary portions of the structure/medium must maintain their position until impacted, at which point only inertial resistance retards motion induced by collision.
How is that? It seems like the equation of motion is great for zero-g or horizontal particulate accretion, but things go awry with vertical motion in gravity because there's no way a portion of a structure - or anything, particulate for that matter - can remain stationary without a constraining force to keep it in place against gravitational force. In a building, that means static self-support capability, scaled by load (non-constant vertically) usually with a considerable margin of safety.
This immediately leads to potential confusion. Once there's a quasi-rigid medium coupled to ground undergoing a vertical collapse, the issue of conservation of momentum becomes quite sticky. Earlier in this thread, [u]I wrote a post that reads like a waffle house menu[/u]... is momentum conserved or not? Akareyon even called me on it at ATS, saying:
from "Akareyon at ATS": "TBH, I read your ponderings "is momentum conserved, yes, no, a little, some more, a little less" and they somewhat scared me..."
My response to this was a little better, I think, but relied on prior background covered in the waffle thread.
I totally understand why that might make you apprehensive, after all isn't it a physical law that momentum is always conserved? Yes, but only if the entire system is considered. Here, the entire system is the building+Earth and, at that scale, momentum is indeed conserved. When ignoring the planet, as we are, momentum is most assuredly NOT conserved. What was the momentum of the rubble pile? Zero. QED.
The tower is coupled to ground. As the upper section begins to descend, the lower section (despite experiencing overload conditions locally) experiences a time-averaged force less than the static load of the upper section. The lower section unloads. As a result, the Earth moves up to meet the falling upper block!
You really want to go there, or would you rather acquire confidence that I'm absolutely correct that momentum is not conserved in the system under study?
and
In the last post, I confirmed that I agree with the basic tenets of classical mechanics by saying momentum is conserved globally but specified correctly that momentum is not conserved locally - at the scale of the tower.
Now, please allow me to tug you back the other way. I claim momentum IS conserved locally at a finer granularity, at least with respect to the slab models I was discussing in the writings which apparently disturbed you, and of the type we're discussing here. An abstraction is that collisions between slabs occur instantaneously, therefore no displacement occurs during collision and no work can be done against coupling to ground. Therefore, momentum IS conserved during collision. Good thing, too, because without some invariant, the mechanical problem cannot be solved.
Now, do you understand the back-and-forth? It wasn't waffling, it was analysis.
It's not an easy notion to understand. I recall seeing a discussion between a cretin I shan't name (this time) and a university physics professor where the prof didn't understand the subtleties of this issue, and broadly claimed momentum conservation inapplicable. Fairly smart people with relevant background don't understand this. What's more, I'd say the jury is still out on precise lines of applicability.
The beauty of a discrete model with 'instantaneous' collisions is that momentum can be assumed to be conserved locally but not globally. Theoretically, it should be possible to move from discrete to continuum in the limit, and converge on stable, uniform properties. Indeed, this is something shagster asserted in the referenced discussion and I've found to be true (for the most part) in all the discrete models I've used.
When going forward with that, however, a couple of things jump out. The continuum formulation above, as far as I know, has not actually been compared with output from a discrete model. The agreement is surmised, but I should like to verify it. The other puzzling thing is that a continuum is founded on infinitesimal action, but does not embody the concept of 'instantaneous' in the same way that the discrete model does. This is worthy of deeper exploration because it really comes down to the same premise which caused the physics prof to believe the problem could not involve momentum conservation, whereas the truth may be subtly different: the continuum problem may not involve momentum conservation.
The import is significant: how can the discrete methods converge on their continuous counterparts if the two stem from entirely different base conservation assumptions? This seems a sure recipe for disagreement, superficially. It should be interesting to resolve this conflict and illuminate the mechanisms at play.
In moving to a continuum, there is no opportunity for or notion of an idealized, instantaneous collision which can accrue mass inertially without doing work against a retarding force. Only the analytical treatment can use this idealization precisely, the slab simulations can only approximate it (fairly well in most cases). While agreement may be good to first order between idealized algebraic discrete models and approximations of such in simulations, the continuum model must directly address this issue whether formulated from the ground up or obtained in the limit of a discrete model.
Examining the formulation above, it would seem there are two approaches to introducing other forms of dissipation:
1) a per-unit-length energy dissipation added at the beginning of the formulation
2) a corrective force added as a term in the final equation
Both suffer from problems. Both leave the issue of momentum conservation itself untouched and are really bringing ad-hoc correction to the issue that momentum really isn't conserved on any level anymore, although the second makes this shortcoming more obvious.
In the first case, a differential measure of mechanical work is not necessary synonymous with accurate accounting for a non-conserving system. This is a subtle trip hazard; intuitively, I think an experienced mechanician would take it as given that there is some analytical or empirically-derived set of terms which can provide a true solution, even if it's practically impossible to specify them. But where is the formal proof of such? I don't know that the actual mechanics of such a non-linear system is captured by this apparently primitive process.
In the second case, there is an immediate problem of 'jumping ahead to the answer' in that a dissipative force term simply added in is of value only when you have data but no analytical treatment. That is, you can say you know there are sinks and what some of them may be, but you don't know how to compute their magnitude. When there is data, it may be possible to to fit experimental coefficients and come up with a very powerful predictive tool, all without significant understanding of the underlying mechanisms. Not so useful in this context.
Since the entire treatment, after energy dissipation is axiomatically introduced through inelastic accretion, is a force-based Newtonian analysis, it will be limited in the same ways compared to an energetic analysis. Traditionally, force methods have been good for treating imposed constraints such as fixed points - a physically unrealizable situation but yet practically true in many mechanical contexts - while energy methods not so much. This is the one plus.
Of necessity due to paucity of data, the first approach is the only viable one. I will assume the correspondence between the approach and whatever the actual mechanics of the system may be. Specifically, this is the assumption that the problem can be solved by the superposition of inelastic accretion plus a variable number of differential displacement sink terms.
Back to conservation of momentum, Part 2
There, now that I've stated it, do you see how weak the assumption is? Where are velocity dependent forces, or more exotic dependencies like material strain, internal degrees of freedom, and thermal wastage? It's a virtual certainty the approach does not capture the true dynamics of any collapsing system!
Inelastic collisions make a whole lot of energy go away, and it's not by magic. It does not disappear, but rather leaves the purvey of the system under study as unexamined/hidden/enfolded variables of state. When a collision is declared inelastic, from the typical view of classical mechanics, it is understood that a literally unknown number of events and interactions occur within the idealized encapsulation of a collision transaction. The key is, below a certain level of detail, it doesn't matter what happens. This is inherent to the very vocabulary of collisions as discrete events between otherwise non-interacting bodies.
The situation of a continuum collapse is the complete opposite. It's no longer even meaningful to talk about 'collisions' between isolated bodies, there is only one body partitioned into abstract infinitesimal segments which are really all integral and intimately connected. Motion of one part, however great or small in size, immediately applies forces to the boundaries above and below that part. There are no collisions. Only motion of a field of matter which is taken to be plastically and irreversibly compressible.
The work done in irreversibly compressing the medium IS inelastic loss. This suggests, even warns, that adding sinks beyond inelastic collision runs the risk of co-mingling sinks at best and over-counting losses at worst. Much has been made of this in the past here and elsewhere but, in retrospect, I find the level of discussion to be crude and unnecessarily seat-of-the-pants. All the same, the problem is real and comprehensive explanation (if it exists) is probably only found in the few articles on collapse. Both Bazant and Seffen have been the target of informal accusations of overlooking momentum conservation and, on the flipside, Gordon Ross and ilk have been criticized for invoking abstract inelastic mechanisms AND inelastic mechanical sinks.
The issue is, inelastic mechanical sinks are one of (or sometimes the only) underlying mechanism behind the inelastic nature of collisions between previously isolated bodies. Again, the infinitesimal elements of continuum matter are not isolated bodies. This is microdetail compared to the traditional treatment of inelastic interactions in physics. On the other hand, while engineering mechanics does include deformation, fracture and other modes of loss and deals with it quite extensively, the context is usually quasi-static and/or not solely driven by internal actions of the studied system but by externally imposed forces.
Homogeneity
It's pretty clear that a discrete model with 'slabs' (particularly disconnected or held in place by virtualized support) does not reflect the actual structure of any whole building. It can approximate (e.g.) floor collapses to some degree of sufficiency, where the material geometry is indeed discretized in some way. It has also shown to be a decent rough first approximation to treating a whole-building system but those rough edges are pretty glaring.
The continuum model, on the other hand, goes to the opposite extreme. It now becomes very difficult if not practically impossible to precisely handle discontinuities and position-dependent properties. Anything but the simplest of expressions for density, dissipative terms, and the like will immediately render the equations of motion analytically insoluble. That's the general benefit of an analytical approach in the first place, besides gaining understanding.
At least there's some hope in the treatment above, although I haven't done it yet. I have done it computationally, and that's where this is all going anyway because it's going to get ugly fast. However, even so, discontinuities are often a problem and specification of piecewise property functions to feed a solver engine decidedly non-trivial effort.
The upshot is that a continuum analysis, unless enormously complex, is going to make a 'smoothie' out of something that really is a heterogeneous configuration of voids and solid shapes having a spectrum of properties. Not automatically a bad or wrong thing, just something to keep in mind.
Both approaches, of course, suffer from the effects of homogenization of both horizontal dimensions to collapse 3D into 1D.
Consolidation with 'discoveries' in the essay with the simple 1 dimensional stacked system game simulation model
Since starting this thread (note: refers to toy simulacra thread), I've learned a lot about this and that, including some things from the experiments conducted and loosely documented here. To me, these were discoveries even if someone had already published on it or even if it was common knowledge in engineering mechanics. Examples are
- convergence of momentum-only to acceleration of g/3
- the fact that a collapse - in it's entirety - really is like a single inelastic collision between the upper part and the lower when the components collide inelastically
The first example led to this latest train of posts; why is there convergence on g/3? The second example has some bearing on developing a more detailed and accurate analytical model, specifically addressing the concerns of the previous posts on how to treat momentum conservation. There appears to be - at least roughly but strongly - the assumed correspondence between model and actual. A linear superposition of inelastic collisions and work done (failing supports) against differential displacement of a system of bodies coupled to ground seems to be pretty much what happens, ignoring any exotic variations like thermal losses or velocity dependence.
I have done quite a few experiments using large numbers of bodies, or stories if you will, both in tall structures and short, and in both analytical and simulation environments. In essence, exploring the transition from discrete to continuous. While not rigorously demonstrated, it appears to be a stable progression to the limit, and means there is an analytical bridge to continuous which only needs to be found.
As mentioned earlier, simulations show a correspondence between a block-driven collapse of a structure and the notion of an inelastic 'collision' between upper and lower sections, with both sections getting crushed in the process and reduced to a compacted volume. In this sense, there is a collision in the conventional physics usage of the term occurring between two bodies, even if not isolated, even if composed of many smaller collisions between components. By stepping back to the global scale, the sequence of collisions which comprise the totality of a collapse can be treated as a single collision, what I'll call the collapse transaction.
Like two flimsy clay structures deforming, compressing and sticking together upon collision, the upper and lower sections are deforming impactors. It is this deformation which consumes energy to be the inelastic sink. These findings apply to a structure in free space, not fixed to ground, although it doesn't matter if there's gravity or not.
This is a statement of the obvious, in some ways. How could a collision between two objects be anything but a collision between two objects? Well, first of all, there are not two physical objects, there are many physical objects. It is technically a many body problem, albeit highly constrained and in the near-singular world of 1D. There are two logical objects, the collection of moving bodies and the collection of stationary bodies. It's a firm, unambiguous definition for the simple systems considered so far but still conceptual rather than actual. The distinction is unimportant for the most part; a compacted region and initial upper block all 'welded' together may as well be a single body, but the moment acoustic physics (the finite speed of stress/strain transmission) or non-rigid coupling of body masses are taken into account, the distribution of mass in at least the lower portion becomes significant.
I shall avoid all of that and treat the continuum problem as a pair of bodies defined by motion or no motion, so logical body is the same as physical body. This is the only thing which makes sense in a continuous media, homogenous or otherwise. Besides, it will be a while if ever before more than one internal state variable representing compaction is considered.
Still, this problem is unlike typical collisions on the subglobal level because material is being exchanged between bodies - the moving body picks up material from the stationary body. This is the accretion part of the problem, and one thing which makes it trickier than textbook examples. Almost all classical mechanics is done with constant mass. A notable exception is the rocket thrust equation which, when suitably inverted, frames this problem surprisingly well. Not exactly the same, though.
The collapse transaction, though not given a name, was mentioned in [u]this post[/u], where it is said:
"If collapse goes to completion in a momentum-only (no supports) inelastic configuration, then the entire event can be considered a single inelastic collision in the sense that the final velocity of the debris pile just before hitting ground is that given by a collision between the upper block and the lower block as point masses - ignoring gravitational effects, of course. So, in a horizontal arrangement of inelastic slabs, a single impactor hitting a line of 99 masses has the collective debris zone speed reduced to 1/100th that at the final collision. Makes perfect sense."
One thing to immediately explore is the quantification of effect of support failure energy when coupled to ground. Ideally, simulation experiment will show that a simple load-displacement response for compaction work added to simple inelastic momentum-only accretion provides an accurate solution.
Bidirectional crushing, compaction
The issue of rigidity of the upper section in the continuum model is essentially the same as in the discrete model, and basically just a choice as far as I'm concerned, not a problem. It is easier by far to have one degree of freedom so that's my starting point.
When considering an upper block which is rigid by decree, the initial upper section need not have any vertical extent, simply be a planar mass of infinite density. This is the same as the discrete model. Therefore, the driver in the first continuum model may simply be an external impulse - a tap on the head, if you will - together with an optional constant force added which represents the initial static load of the upper section. Mechanically equivalent under some circumstances.
The accumulated debris or compacted zone, in motion with such a 'rigid' upper section, will naturally have spatial extent in cases of finite compaction. Also, like the discrete model, infinite compaction is just the setting of one parameter, so it can be done as a bounding case. We tend to think of material being compacted when its volume is reduced, but mathematically this is the same as having a stretch (reciprocal of compaction) of between 0 and 1. This representation is more convenient for calculation and avoids the singularity of infinite compaction because such is represented as zero stretch.
Academic: Having negative compaction, strangely enough, may be useful and even physically meaningful when interpreted as interpenetration. Stretch greater than 1 - which corresponds to real stretch in tension - is of doubtful value in compression unless you're dealing with release of potential energy by the trigger of pressure or applied force, like an explosive. This would correspond to 'Jiffy popping' on contact.
With respect to crush direction and compaction, little if anything new is introduced by going to a continuum.
That's a lot of words without any graphics. Might be nice to see a picture. Here are graphs of position versus time and velocity versus time from the solution of the equation of motion derived above:
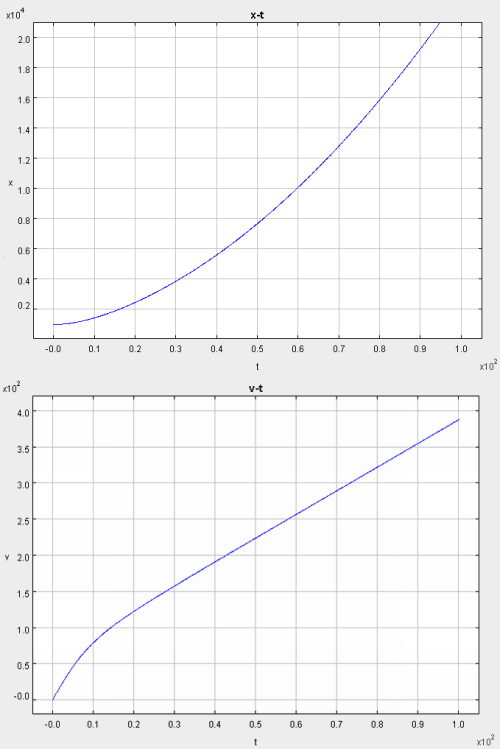
This was solved numerically and graphed using ODE Toolkit, which is free. Again a nod to shagster. I downloaded this program because I'd read his posts where he describes solving this very problem with the tool, and it's the only thing I've ever used it for. The post where shagster shows the setup and solution is here, I can't do a better job of explaining it:
http://www.physforum.com/index.php?showtopic=12383&view=findpost&p=172801
I did exactly the same as shagster, except the run length was 100 seconds to allow terminal acceleration to fully manifest. Sure enough, when I do an eyeball measurement of the slope of the velocity graph from 30 to 90 seconds, I get 3.3 m/s², which is not one-third g but close and converging from the right direction.
There is no easier way to play around and get a solution of simple first order ODEs than this product, I just don't do that sort of thing much. On those rare occasions where I have solved differential equations lately, they've been more conveniently set up in other environments like Euler/Maxima and Modelica (also both free). This program, while extremely limited in functionality, is quite simple to use by comparison. I'd encourage anyone interested to download and replicate.
This is very easy, you don't even need to know what you're doing let alone solve a differential equation. Getting an analytical result of g/3 is not as easy, though maybe not hard.
ODE Toolkit is nice and definitely easy to use, but is also buggy and user-hostile in a few respects. Doesn't do much beyond solving and graphing, no tabular data and picture export only to PS. However... that easy part is SO easy that it takes about a half hour to explore the close relatives of this equation. For instance, solutions of the equation with added coefficients of terms in v/x, v^2/x, v and v^2:
v' = 9.81 - r*v/x - s*v^2/x - a*v - b*v^2
x' = v
r,s,a,b are constant coefficients
There is, at least at the moment, no physical motivation for this form of equation but it's interesting to check out the variations anyway.
(Please note that, while I chose y as coordinate of motion for the derivation, since it's customarily associated with vertical in most applications, the programs wants the base dependent variable to be x.)
Effects of coefficients r, s, a, b
Of the coefficients r,s,a,b listed in:
v' = 9.81 - r*v/x - s*v^2/x - a*v - b*v^2
x' = v
r,s,a,b are constant coefficients
these are the effects, or very nearly so:
r => constant acceleration, increasing r is decreasing acceleration
s => terminal acceleration, increasing s is decreasing asymptotic value
a => terminal velocity, increasing a is decreasing time to max and increased max velocity
b => terminal velocity, increasing b is decreasing time to max and increased max velocity
Of the coefficients r,s,a,b listed in:
v' = 9.81 - r*v/x - s*v^2/x - a*v - b*v^2
x' = v
r,s,a,b are constant coefficients
these are the effects, or very nearly so:
r =>
terminal acceleration, increasing r is decreasing asymptotic value
s => terminal acceleration, increasing s is decreasing asymptotic value
a => terminal velocity, increasing a is decreasing time to max and increased max velocity
b => terminal velocity, increasing b is decreasing time to max and increased max velocity
Corrected. The non-constancy of acceleration is not apparent at small values of r, but it's there.
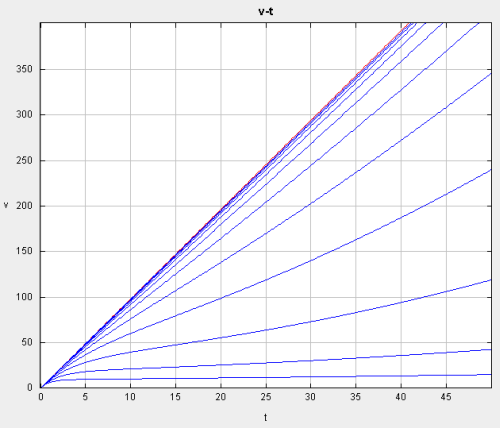
While I don't think this sort of analysis has much to do with any of the 9/11 collapses in their entirety, it might be pretty good at characterizing some of the verinages where there really is block vs. block. Also, I actually see the potential for describing an interior floor collapse, at least in the sense of fitting parameters to actual data.
Where this technique might work - should work - is any case where there is uniform engagement of colliding parts, as in floor slab sections dropping onto equal size slabs or whole building top dropping squarely on the bottom.
Back to conservation of momentum, Part 3
1) a per-unit-length energy dissipation added at the beginning of the formulation
2) a corrective force added as a term in the final equation
Revised appraisal: Either way is okay up to the limits of what they're capable, but #2 is capable of more and is better; I'll say why later but, in a nutshell, it's a perfectly valid approach (in contradiction to some of my earlier comments) and is more flexible. I've also solved the imaginary conundrum of the momentum conservation going to the continuum limit - it's not a problem. And so there is at least some physical motivation for this form:
a = 9.81 - s*v^2/z - a*v - b*v^2
The term with s coefficient is the momentum transfer term and the two velocity dependent terms could be interpreted as viscous drag and turbulent drag, respectively. Sorry for switching around the displacement coordinate, now I show it as z, but I've been talking this up with Benson too and he objects to y for vertical. Which reminds me that Benson's avalanche theory, which is based on fitting drop data, indicates the term in v is not needed or counterproductive. So, no viscous drag. His model also indicates nothing in the way of structural resistance contributed, either.
Honestly, before all is said and done, I'll probably re-derive Bazant's simple analysis from scratch and certainly be in a better place to have another look at what Seffen did. A complete rederivation of the basic mechanics will open up exploration of the parameter space, making it a living analysis instead of a snapshot as applied to the towers.
I always thought the 1D models of the type here would be good for characterizing verinage. After all this time spent dabbling, I look back on many arguments on this subject as being so primitive. Even at this forum, and from me, though less so than what you generally see.
Why does verinage decelerate but the towers do not? Look at the buildings!
1) Concrete slabs fracture to remain as fragments with shorter effective average length but also greater capacity
2) Concrete slabs have a different load-displacement response under compression and bending
3) Cellular geometry ensures higher cross-sectional load bearing surface during disorder of collapse; is relatively insensitive to misalignment
4) Cellular geometry has a greater tendency to trap air in the interior
Don't discount #4. Pressure builds quickly if the air doesn't escape. The compaction acts (quickly) to close off flow paths to the exterior yet the pressure increase wants to open the orifice wider, even if that means blowing chunks out. There will be a point of dynamic equilibrium on this alone. #4 is not something that will cause deceleration in itself, but it becomes a large factor as the collapse progresses. Since the acceleration is due to the sum of forces, a high magnitude in this category sharply limits the acceleration - rolls it off like the curves above.
#2 and #3 don't necessarily cause deceleration in themselves, either. They are reasons why the global load displacement response would be a greater magnitude in relation to a given static DCR.
It is #1 which has the greatest potential to produce a consistent average resistive force which exceeds the static demand. That favors propagation over compaction and means the crush front can reach ground faster, perhaps a lot faster. In a tall tower, that doesn't matter for a long time, if ever (because of mass lost outside of footprint).
In these short apartment buildings it can reach ground quickly and, at that point, the mode goes to exclusive crush-up (no matter what mix of up and down it was before) and the rules change a bit. Compaction continues to some degree but remaining uncompacted stories are favored to crush, if anything at all is going to crush. The driving mass is now much smaller.
Crush up exhibits a tail-off of velocity (theoretically, ideally) to zero. That means deceleration! The shorter the building is and the greater the effect of #1, the sooner this commences and the faster the rate.
Acceleration converges on g/3
David Benson gave me the answer on how the value of g/3 is determined from the equation of motion in the OP.
Respective of the physically correct formulation (where it certainly should not matter which approach one uses), consider the governing equation a = g - v^2/z to assume that for large t one has approximately v = kt with a = k. It follows that
z(t) = z0 + (1/2)kt^2
and for t sufficiently large z0 can be neglected. Then
k = g - (kt)^2/[(1/2)kt^2] = g - 2k;
k = g/3.
Have to use a different governing equation to obtain Seffan's result; indeed I believe he does derive something different.
That post was at physforum.
http://www.physforum.com/index.php?showtopic=12383&view=findpost&p=510877
Here goes. If the value of acceleration converges on a constant, then for large t ( the independent variable) the relationship v = at is approximately correct. This is the familiar formula for determining velocity under constant acceleration. So, if the convergence actually occurs, we can work with this simplified formula to obtain a value for acceleration. Otherwise, it will lead to a contradiction (like z=z^2 or 3=5 some such).
Benson uses v = kt with k representing the constant acceleration we'll assume equates to a. To find the position as a function of time, v = kt can be integrated once to give:
z = z0 + (1/2)kt2
also a familiar formula for position change under constant acceleration. The constant offset from integration z0 is the initial position which can be taken to be well after the onset of constant acceleration (really, wherever you want) and, if you let t range MUCH larger than that, z0 can be ignored because (1/2)kt2 will be much larger. Now the value of z under a long period of constant acceleration is approximately:
z ~ (1/2)kt2
Even though we're considering the limit of very large t, the original equation of motion still holds as always, whether or not the assumption of constant acceleration is true, so that relation can be used. Plugging in the values of a, z and v from the large t approximation into the eq of motion should yield either a meaningful result or a contradiction.
eq of motion: a = g - v^2/z
Let a = k, v = kt, z = (1/2)kt2
=>
k = g - (kt)2/[(1/2)kt2]
=>
k = g - 2k2t2/kt2
=>
k = g - 2k
=>
k = g - 2k
=>
3k = g
=>
k = g/3
Start by assuming the constant relation and obtain formulas for the dynamic variables; then plug into original equation and see what comes out.
The assumption of (near) constant acceleration at large t holds true for g/3.
Another approach:
For very large t,
a goes to k
v goes to m +kt
z goes as p + qt + 1/2 k t^2.
If plugged into the a(v, z) term in the limit of very large t, k goes to g/3.
Same idea. Makes sense.
For the equation of motion
a = a(v,z) = g - v^2/z
We are saying the last term converges to 2g/3 for large t.
That is neat. v^2 in the numerator and z in the denominator increase at the exact same rate for very large t. The motion can be understood as a balancing act between v^2 and z.
Did anyone solve the diff eq for z(t)?
It isn't hard to see the shape of a, v and x from the simple relations expressed in the diff eq.
curvature = g - slope squared over position.
How many functions could look like that?
Right now, the treatment of this essay does not include:
- energy sinks of any kind other than momentum
- non-uniform density
- finite compaction ratio
- mass loss
and that's a lot missing. When it gets all of that, I suspect it will look like Bazant. Any variation would hopefully be a more general framework for examining accretion problems than the WTC-centric stuff so far.
Interpreting the velocity dependent sinks as drag may be semantics, if this form is correct, or it may not. The velocity dependent sinks like pulverization, which is more appropriate to the system, may have a slightly different form.
___________________________________________________________
1 Originally posted by OneWhiteEye here